How to Calculate Square Root in Excel (3 Easy Ways + VBA)

Hello there citizen of Excel town! Here's a brainwave. Have you ever thought about getting Excel to do what you have been doing for a good chunk of your school life on a calculator? We're sure you've been there, and so have we. Let's pick something easy, say, square root! Not only can you calculate square roots in Excel, but you also have a bunch of options to choose from.

In today’s tutorial, you will be shown how to calculate the square root of a number using the SQRT and POWER functions and VBA. For calculating the nth root (including square root), we will show you how to work with the exponential operator. Sounds like a square deal?

Let’s get calculating!

Recommended Reading: How to Insert Square Root Symbol in Excel

Method #1 – Using SQRT Function

We begin calculating square roots in Excel and what’s better for calculating square roots than a square root function? Quite little else. The SQRT function takes only an argument, a number, to return the square root of that number. Very straightforward. Let’s see how it goes, the simple formula is:

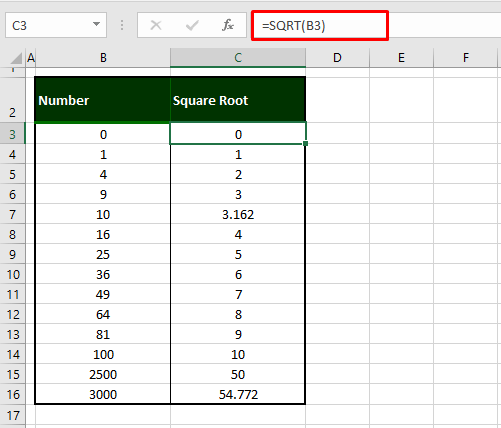
The SQRT function can be provided a number or the cell reference of a number for it to return the number’s square root. In the example ahead, we have a set of numbers in column B and need to calculate their square roots, returned in column C. The first number we have supplied to the function is the number 0 in cell B3. 0’s square root has been returned as 0.

Let’s take another example. B8 contains the number 16 and the SQRT function returns its square root as 4.

Method #2 – Using Exponential Operator

See this number 2³

The little 3 is the exponent and it means that the number 2 is raised to the power 3. Now if we can raise this number to the power 0.5 or 1/2, we will have the square root. Similarly, in Excel, the caret symbol “^” can be used as an exponential operator to raise a number to a power. Use the formula below with the exponential operator to calculate the square root of a number:

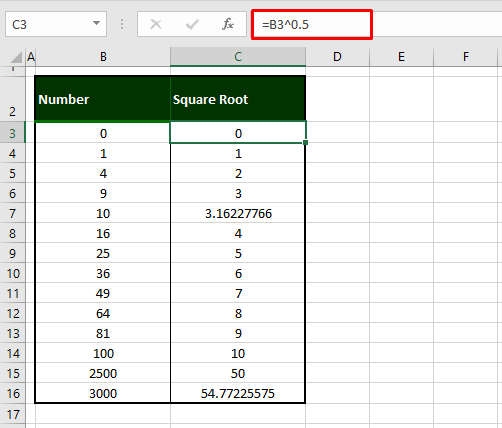
B3 contains the first number we’re calculating the square root of. By reference, the number 0 has been raised to the power 0.5 (or 1/2) using the exponential operator ^. With this symbol as the exponential operator, we have arrived at the square root of the numbers in our example:

Method #3 – Using POWER Function

The square root of a number can also be calculated using the POWER function. The POWER function returns the result of a number raised to a power. This is similar to using the exponential operator as both raise the number to a given power.

Since we’re finding the square root, we can enter the power of a number as “0.5” or “1/2”. We will show you how to use the POWER function to calculate the square root with this formula:

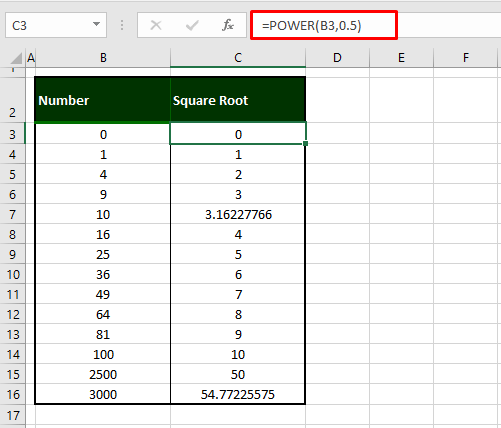
For the first parameter, enter the number whose square root you want to find, we’ve entered the first one from our example i.e. B3. The second parameter will be the power by which you want to raise the number. For calculating square roots, the number will need to be raised to the power 0.5 or 1/2. The square root of the following numbers has been calculated using this formula with the POWER function:

Method #4 – Using VBA

If you’re interested in hopping off your spreadsheets for a bit, you can calculate the square root using VBA. VBA is used for automating tasks in Office applications. Therefore, we’ll assign the task of calculating a number’s square root to VBA. The detailed steps for this are as follows:

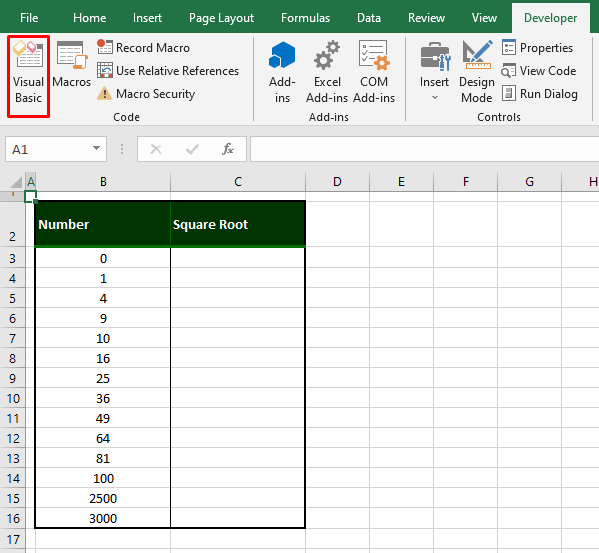
• Go to the Developer tab and select the Visual Basic icon in the Code
• Alternatively use the keyboard shortcut Alt + F11 if you haven’t enabled the Developer tab.
• 
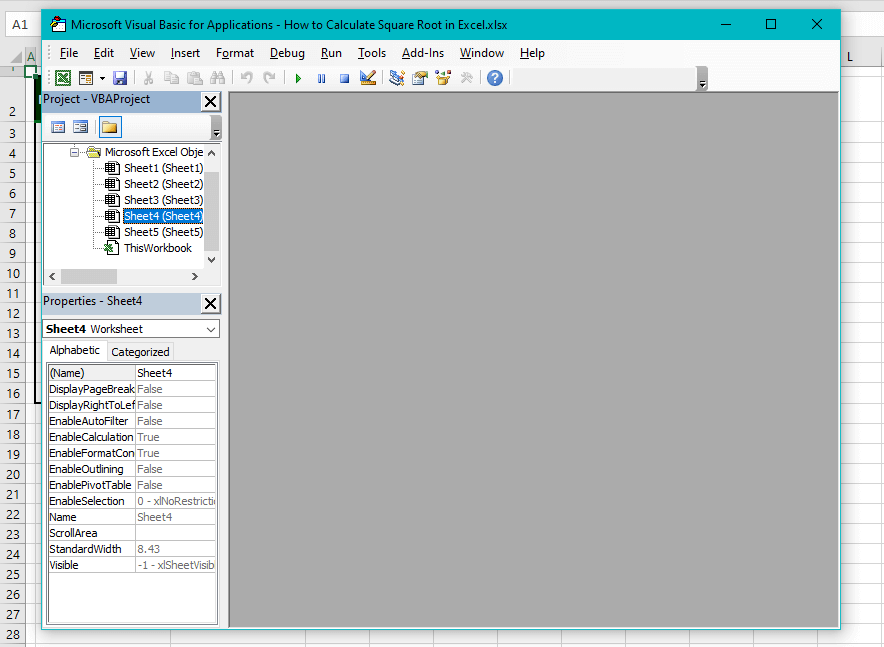
• The VB editor should open now and this is what it looks like:
• 
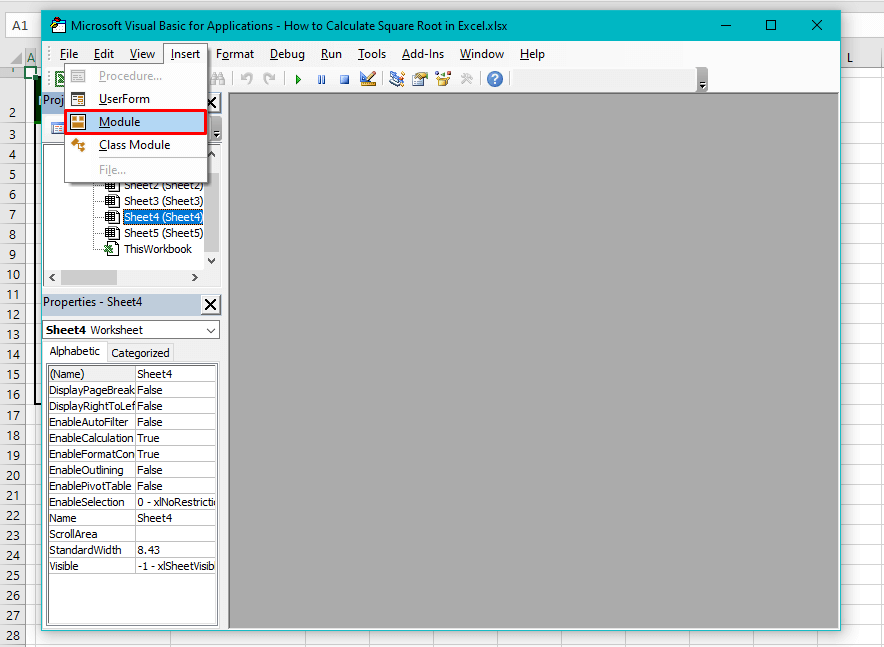
• Now select the Insert tab and click on Module from the menu.
• This will launch a Module window.
• 
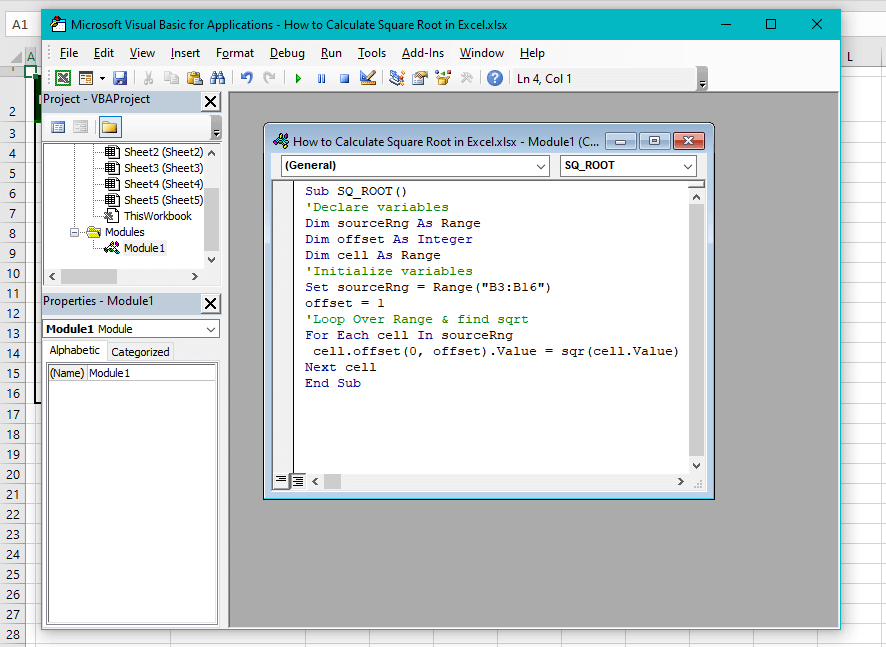
• In the Module window, copy and paste the following code:

• Sub SQ_ROOT()
  'Declare variables
  Dim sourceRng As Range
  Dim offset As Integer
  Dim cell As Range
  'Initialize variables
  Set sourceRng = Range("B3:B16")
  offset = 1
  'Loop Over Range & find sqrt
  For Each cell In sourceRng
   cell.offset(0, offset).Value = sqr(cell.Value)
  Next cell
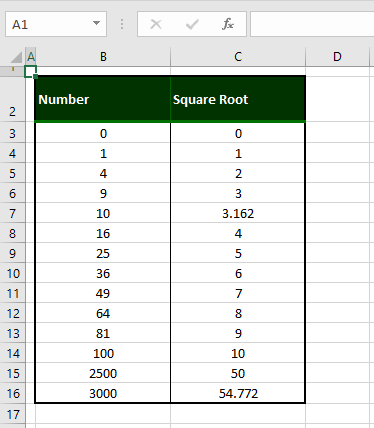
  End Sub

  This code will take the values from B3:B16 and generate their corresponding square roots in C3:C16.To modify this code as per your worksheet, change the 'sourceRng' variable value in the code to the cell range for which you intend to find the square root.
  Changing the 'offset' variable value will help you to define the target cells where you wish to populate the results.

• Press the F5 key to run the code and you will get all the square roots populated.

Calculating Cube Root or Nth Root

If you are to calculate the cube root or nth root of a number, it’s all too easy with the exponential operator. For the nth root, raise the number to the power 1/n. The formula to calculate the nth root will be:

Number^(1/n)

Let's demonstrate how to calculate the cube root, the 4th root, and the 5th root using the formula above as a basis.

Calculating Cube Root

Use the formula ahead to calculate the cube root:

The formula involves the number in B3 for the calculation of the cube root. Next, we use the exponential operator to raise the number 0 to the power 1/3 enclosed in parentheses. This will return the cube root of 0 as 0. The cube roots for the rest of the numbers in our example are shown below:

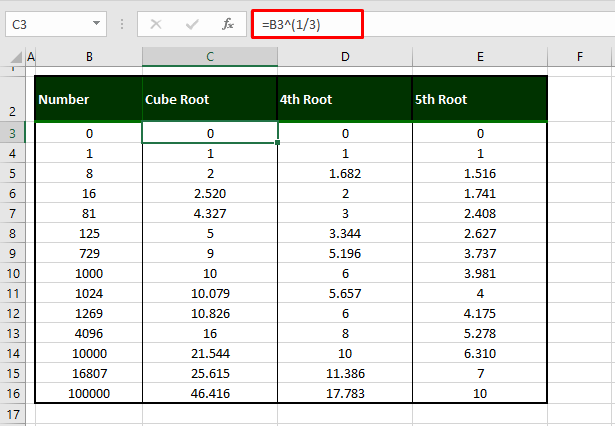
Calculating 4th Root

Let’s use the formula of the nth root to find the 4th of the same numbers:

For the 4th root, we have traded the denominator of the power with the number 4. Below are the calculated 4th roots of the numbers in column B:

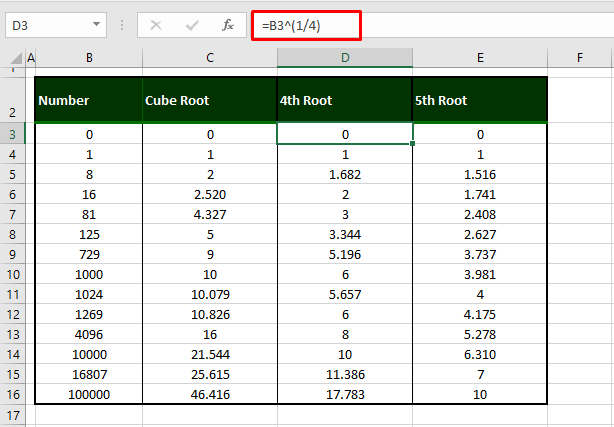
Calculating 5th Root

Let’s see another example of calculating the nth root of a number. With the following formula we will aim to calculate the 5th root:

With the number in B3, by using the exponential operator, we have raised the number to the power 1/5. This formula will return the 5th root of B3 and ahead you can see how it applies to the other numbers in our example:

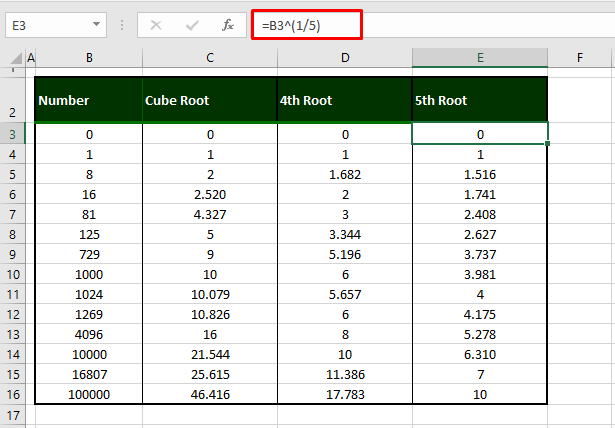
That was fairly and squarely the lot of what we had to say about calculating square roots in Excel. Did you feel like you were taken back to square one in mathematics? For something like this next time, it’s quite unlikely that you’d have a calculator around you but you do have Excel and the many ways to calculate the square root. That was today’s brain food. We’ll be back with more Excel soup for the mind!